Inhaltliche Analyse auf Journal-Ebene

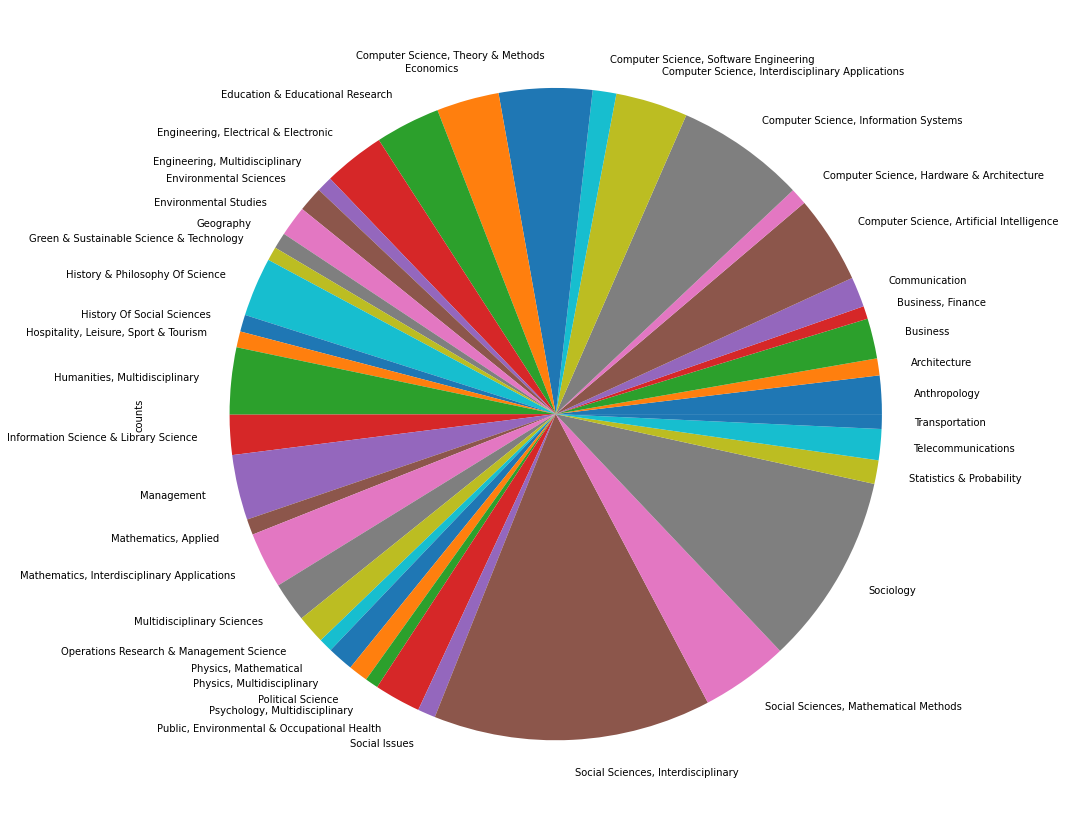
Vor der Erstellung der Netzwerke möchten wir die fachliche Zusammensetzung des Korpus beschreiben. Um einen ersten Eindruck der vertretenen Disziplinen zu erhalten, nutzen wir die den Journals und Büchern zugeordneten WoS_Categories und schauen uns die Verteilung dieser im Datensatz an. Da ein Journal, bzw. Buch bis zu sechs Kategorien zugeordnet sein kann, müssen diese in einem ersten Schritt aufgesplitted werden.

import pandas as pd
import re

# Korpus einlesen (Datei inkl. unvollständige Einträge)
corpus = pd.read_csv('corpus/corpus_all_entries.csv', low_memory = False)

# Neuen Dataframe anlegen, um WoS_Categories zu analysieren
df_neu_cat = corpus[corpus['wos_cat'].notnull()]
# WoS-Kategorien am Semikolon trennen & als neue Spalte in den Korpus einfügen
splittedCategories = df_neu_cat['wos_cat'].apply(lambda row: row.split(';'))
corpus.insert(0,'splittedCategories', splittedCategories)
# Explode Dataframe anlegen, um die Kategorien zu zählen
df_exp_cat = corpus.explode('splittedCategories', ignore_index=True)
df_exp_cat['splittedCategories'] = df_exp_cat['splittedCategories'].str.strip() # Leerzeichen entfernen

# Einzelne Kategorien zählen 
pd.set_option('display.max_rows', None)
df_exp_cat.splittedCategories.value_counts().to_frame('count').sort_values('count', ascending=False)

# Das value-counts Output als eigenes Dataframe ausgeben
df_plot_cat = df_exp_cat['splittedCategories'].value_counts().rename_axis('cat').reset_index(name='counts')
df_plot_cat = df_plot_cat.drop(df_plot_cat[df_plot_cat.counts <= 500].index) # Werte <500 löschen
df_plot_cat.groupby(['cat']).sum().plot(kind='pie', y='counts', figsize=(15,15), legend=False)

<AxesSubplot:ylabel='counts'>

# Kategorienkombinationen zählen 
pd.set_option('display.max_rows', None)
combi_count = corpus.wos_cat.value_counts().to_frame('count').sort_values('count', ascending=False)
combi_count.loc[combi_count.index.str.contains(';') == True]

Die Disziplinen, die am häufigsten vorkommen entstammen der Soziologie, den interdisziplinären Sozialwissenschaften und der Computer Science. Hierbei ist bemerkenswert, dass “Social Sciences, Interdisciplinary” vergleichsweise sehr groß ist und mit über 10,000 Einträgen doppelt so viele Veröffentlichungen enthält als die dritte Kategorie “Computer Science, Information Systems”. Die hohe Anzahl sozialwissenschaftlich kategorisierter Publikationen lässt sich u.a. durch den Search String erklären, der explizit in diesen Disziplinen nach Netzwerkliteratur gesucht hat. Besonders interessant ist, dass an sechster Stelle “Social Sciences, Mathematical Applications” steht, was einen transdisziplinären Zusammenschluss zwischen Natur- und Sozialwissenschaften andeutet. Physik als expliziter Begriff steht erst an Stelle dreiundzwanzig, häufiger kommen Disziplinen aus der Computer Science vor. Außerdem fällt auf, dass wirtschaftswissenschaftliche Disziplinen ebenfalls recht weit oben stehen.

Insgesamt führt die Analyse der verschiedenen Wissenschaftsdisziplinen im Korpus zu erwarteten und daher recht plausiblen Ergebnissen. Die Disziplinen, die wir in unserer Untersuchung fokussieren, führen die Häufigkeitsverteilungen an, wodurch sich vermuten lässt, das wir mit unserem Search String die richtigen Disziplinen erfassen konnten.

# Jahresverteilung für ausgewählte Kategorien ansehen
df_socialscInter = df_exp_cat[df_exp_cat.splittedCategories == 'Social Sciences, Interdisciplinary']
d = len(df_socialscInter.index) # Teiler um zu normalisieren
df_socialscInter = df_socialscInter.groupby(['publ_year']).size().div(d).to_frame('Social Sciences, Interdisciplinary')
df_sociology = df_exp_cat[df_exp_cat.splittedCategories == 'Sociology']
d = len(df_sociology.index)
df_sociology = df_sociology.groupby(['publ_year']).size().div(d).to_frame('Sociology')
df_physics = df_exp_cat[df_exp_cat.splittedCategories == 'Physics, Mathematical']
d = len(df_physics.index)
df_physics = df_physics.groupby(['publ_year']).size().div(d).to_frame('Physics, Mathematical')

# Relative Häufigkeit von drei Kategorien anzeigen, um Unterschiede im Wachstum festzustellen 
ax = df_socialscInter.plot()
df_sociology.plot(ax=ax)
df_physics.plot(ax=ax)

<AxesSubplot:xlabel='publ_year'>

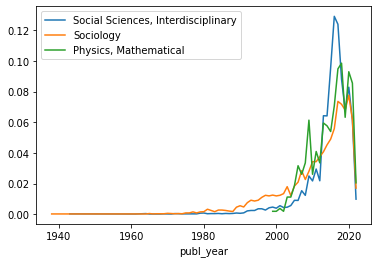
Auch die zeitliche Analyse ausgewählter WoS_Categories liefert plausible Ergebnisse. Da die Werte normalisiert wurden, kann hier allerdings keine valide Aussage über die relativen Häufigkeiten gemacht werden, vielmehr steht das Wachstum der Kurven im Fokus. Hierbei ist am frühesten ein Anstieg der Sociology ab circa den 1970ern zu sehen, was im Einklang mit der beschriebenen Literatur steht. Ab kurz vor der Jahrtausendwende taucht die Kategorie Physics, Mathematical auf und steigt schnell stark an, was ebenfalls mit der Literatur übereinstimmt. Die Kategorie Social Sciences, Interdisciplinary läuft mit der Kurve der Sociology mit, steigt jedoch erst später, aber dafür steiler, an. Da aus der Literatur schon recht früh der Einfluss von u.a. Politolog:innen, Psycholog:innen und Anthropolog:innen hervor geht, scheint auch diese Kurve plausibel. Der steile Anstieg ab den 2010ern ist jedoch aus der beschriebenen Literatur nicht ganz erklärbar und könnte in den weiteren Analyseschritten weiter untersucht werden.